….also known as the Lean Equation
Figure skating is all about riding edges in circles, like a bicyclist riding in a circle. This can be analyzed from two reference frames: that of a stationary observer, or from the non-inertial reference frame of the skater.
From the observer’s reference frame: we know from a study of planetary orbits that circular motion requires a constant pull toward the center of the circle, which is called the centripetal force. For a skater with linear velocity $v$, then the centripetal force $F_c = \frac{mv^2}{r}$ where $v$ is the skater’s linear speed around the circle and $r$ is the radius of the circle.
It is convient to continue our analysis from the skater’s reference frame. After all when we skate, we aren’t really doing anything most of the time. We push onto an edge, hold as the world revolves around us, and then some time later we make a transition and push onto a new edge. So from the skater’s reference frame: it is a non-inertial reference frame because it’s not moving a straight line. Therefore there will be fictitious forces. Fictitious because they are not really how things work (from an inertial reference frame), but if we include them we will get the right answer.
In this case, the fictitious force is the centrifugal force, which is the same magnitude and formula as the centripetal force, except it is directed outward from the circle. We can now analyze the forces, whether real or fictitious, operating on our skater from the skater’s non-inertial reference frame. We can consider to skater to be a point mass at the center of gravity (approx. belly button), and then $L$ distance between that center of gravity and the skate touching the ice.
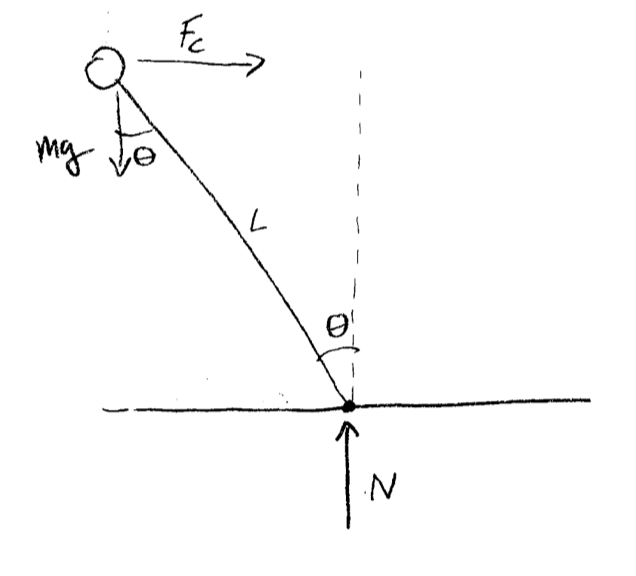
- Centrifugal force $F_c = \frac{mv^2}{r}$ acts outward on the skater, from the center of gravity.
- Gravity $F_g = mg$ acts downward on the skater, from the center for gravity.
- Normal force $N$ acts upward on the skater, at the skate-ice contact point, to exactly cancel out the vertical component of gravity. Note that the ice is only able to push the skater up, but not sideways.
The skater is leaning into the circle with angle $\theta$, and l
Lets’ assume the skater is stationary (in our non-inertial reference frame), i.e. not falling over. Gravity and the centrifugal force both cause a torque around the skate: gravity to make the skater fall over, and centrifugal force to push the skater back toward the vertical. Since the skater is stationary, both torques must be equal. Recalling that torque equals linear force (perpendicular to the lever) times length of the lever, we have:
- Clockwise Torque from Centrifugal Force: $L F_c \cos \theta$
- Counter-Clockwise Torque from Gravity: $L m g \sin \theta$
Setting these two equal we get: $$F_c \cos \theta = m g \sin \theta$$ This simplifies to $$\frac{v^2}{rg} = \tan \theta = \frac{\omega^2}{g}$$ where $\omega$ is angular velocity (in radians per second). For small angles $\tan \theta = \theta$, therefore we. can think of this equation as $$\frac{v^2}{rg} = \theta = \frac{\omega^2}{g}$$.
As skaters we can gain insight from this:
- Most of the time skating we don’t do anything, we just hold an edge while the world revolves around us.
- From the observer’s reference frame, we are both orbiting the center and turning around our own axis, making one revolution per orbit. Therefore, the inherent act of skating on a circle gives us angular momentum, which can be used elsewhere for various steps including spins and jumps.
- Figure skating involves leaning into the circle. In some cases our whole body leans in a straight line, whereas in other cases we may have only the lower body lean and hold the upper body vertical. That lean may not feel like a lean because our body is in line with the “effective” gravity vector. Thus, skating exists with a sense of aplomb, or relationship to the vertical, with the “vertical” understood to be modified based on the circle. More on this later…
- The amount of lean depend on speed and circle size. Larger circles at the same speed require less lean. That is why it is so hard to stay on small circles if we are skating fast.
- Assuming a constant skating speed, you can control the circle size by the amount of lean. If you start to slow down, you can maintain a constant lean and spiral in; or else maintain a constant circle and go increasingly upright. But you cannot do both.
- If you skate a figure too slowly, you will double track on your flats. Thus there is a minimum speed to maintain a clean edge.
- None of this depends on the skater’s height (Note that $L$ cancels out of the equations). There is no physical support for the notion that the optimal size of a figure 8 circle is 3 times the skater’s height. There is reason to believe it would have to do with the radius of the rocker (which as the skater leans more, will lean down onto the ice).
Try On The Ice
- Push onto a steady forward outside edge, hold things steady, and then play with the amount of lean in your upper body. See how you can “steer” things to make a larger or smaller circle through these adjustments.
- Compare pushing onto a steady edge with “regular” vs. “reverse” check of the shoulders. What does the physics say about how these two experiences should compare. Does this comport with what you observe? What are some possible reasons why changing the check of the shoulders would affect the size of your circle?
- Put yourself into a one foot spin, observing the lean and thinking about this question: As you enter the spin, you lean over further ($\theta$ increases) and spiral into a smaller circle. But as the circle gets smaller and smaller into a true spin, you no longer lean further over, but now come to a true vertical. What’s going on? (This will be examined further in the future).